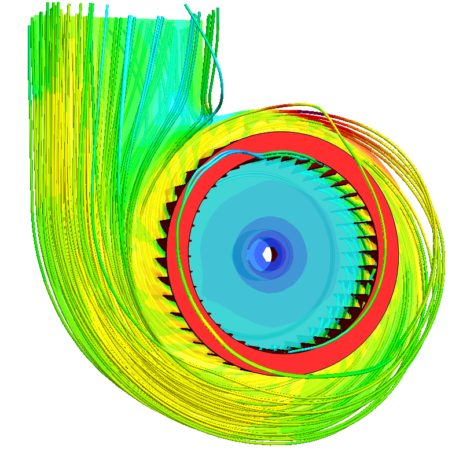
Metodo CFD Fluidodinamica Computazionale
Analisi CFD
-------------------------
Analisi FEM
-------------------------
Vantaggi FEM/CFD
-------------------------
Cinematica
Fluidodinamica Computazionale
La fluidodinamica computazionale è l'insieme di tecniche che, attraverso l'ausilio di sistemi computazionali, permettono di simulare la dinamica dei fluidi.
La fluidodinamica computazionale risolve in modo efficiente i problemi di flusso e di termodinamica nei fluidi: calcola le grandezze fluide (forze, pressioni, velocità, temperature, etc) e consente di accedere alla conoscenza dei fenomeni attraverso rappresentazioni grafiche, mappe, diagrammi e valori numerici che possono essere rappresentati su punti, superfici o volumi.
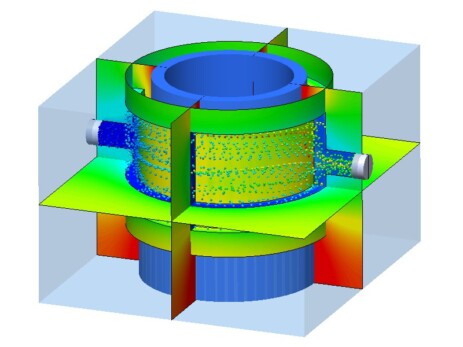
Si utilizza la fluidodinamica computazionale per tutte le problematiche che coinvolgono l'azione di fluidi e per i quali un calcolo secondo le formule "classiche" risulterebbe impraticabile.
Il calcolo CFD si applica, per esempio, nello studio dell'aerodinamica (automobili da competizione, aerei, razzi) , nello studio di pompe, turbine, motori e valvole, negli impianti, nell'analisi di comfort ambientale, etc etc.
La fluidodinamica computazionale fornisce vantaggi ai progettisti in un'ampia gamma di settori, quali
- settore aerospaziale
- settore automobilistico
- scienze biologiche
- medicale
- macchinari
- high tech
- ambientale
- ...
A differenza dei problemi lineari in cui la risposta di un sistema è proporzionale all'input fornito, la fluidodinamica è un problema altamente non lineare e questo comporta che la risposta del sistema sia difficile da predire.
I casi risolti con formule chiuse in fluidodinamica sono molto pochi. Quindi, storicamente, si è cercato un metodo per risolvere il problema del comportamento fisico dei fluidi.
L'introduzione dei sistemi computazionali ha segnato un grande passo scientifico ed ingegneristico e ha permesso di aggredire il sistema di equazioni che sta alla base della teoria dei fluidi: Navier-Stokes.
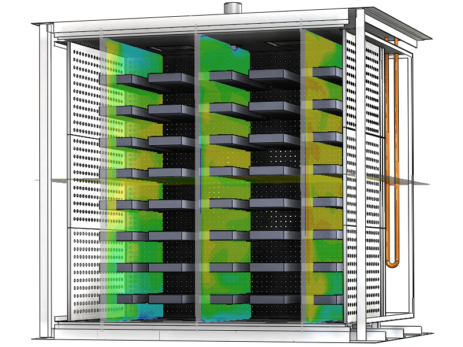
Per risolvere un sistema di fluidodinamica computazionale CFD si devono unire due componenti fondamentali:
- modelli fisici
- metodi numerici

Il calcolo fluidodinamico si basa su un sistema di equazioni differenziali di Navier-Stokes.
Queste equazioni di basano su principi classici dell'analisi dei sistemi:
- legge di conservazione della massa: massa entrante, uscente e generata
- legge di conservazione della quantità di moto: variazione della quantità di moto e forze agenti
- legge di conservazione dell'energia: variazione di energia interna, lavoro e calore
Inoltre, sono presenti delle ipotesi aggiuntive:
- il fluido è approssimabile ad un continuo, ovvero non si considera la struttura molecolare ed il suo movimento oltre certi livelli di scala
- le proprietà macroscopiche del fluido esaminato non sono influenzate dalle molecole
- le proprietà del fluido sono descritte da funzioni nello spazio e nel tempo
La soluzione del sistema di equazioni di Navier-Stokes permette di calcolare il campo fluidodinamico di un sistema.
Pur essendo un sistema "facile" da comprendere, la soluzione matematica è di difficile trattazione se non per pochi casi particolari.
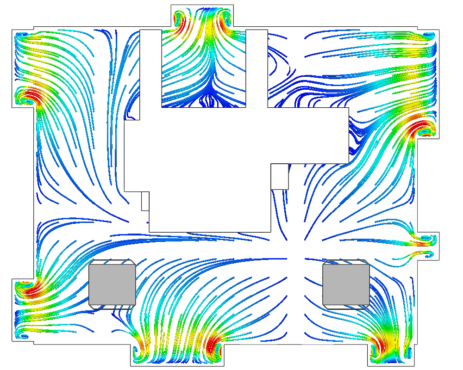
La lista non è esaustiva, tuttavia presenta un notevole porzione delle possibilità di calcolo.
- liquido
- solido
- gas reale
- transitorio
- turbolento
- k-omega
- SST
- LES
- DES
- incomprimibile
- esterni
- rotazionali (1 DOF)
- movimento prescritto (da 1 a 6 DOF)
- DFBI (denominazione che varia in base al software)
- Overset
- Harmonic balance
- convezione (naturale e forzata)
- irraggiamento
- trasferimento termico nei solidi
- trasferimento termico coniugato tra fluidi e solidi (CHT)
- fluidi multifase (presenza di fluidi e gas)
- fluidi con particelle in sospensione
- particelle sospese 2-way coupling
- particelle discrete (DEM)
- calcolo lagrangiano
- calcolo misto euleriano-lagrangiano
- VOF
- condensazione
- regime transonico
- regime supersonico
- FSI 2-way coupling
- Moto prescritto del solido nel fluido
- Moto indotto del solido dal fluido
- non premiscelata
- parzialmente premiscelata
- EBU
- PPDF
- chimica complessa
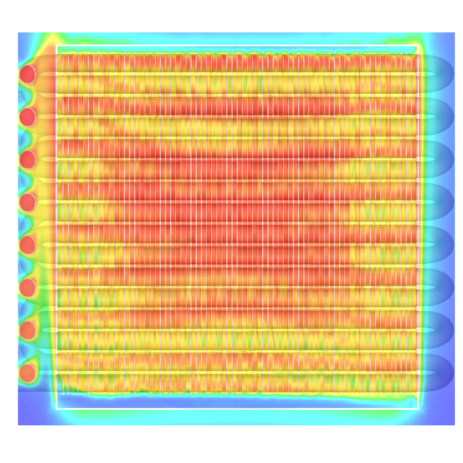
La fluidodinamica computazionale presenta una complessità elevata per via della grande quantità di fenomeni che si possono simulare.
Tuttavia i vantaggi che ne derivano sono molteplici:
- misurazione di grandezze di difficile rilevazione per via sperimentale
- misure su tutto il volume/dominio di calcolo (per via sperimentale è possibile misurare grandezze solo in certi punti)
- valutazioni preliminari dei sistemi già in fase di progetto
- riduzione del ricorso a prototipi
- possibile complemento a studi sperimentali per avere una visione allargata dei fenomeni in atto.
Alla fine si ha una riduzione dei tempi di progettazione, di primaria importanza nelle attività odierne.