Analisi CFD
-------------------------
Analisi FEM
-------------------------
Vantaggi FEM/CFD
-------------------------
Cinematica

Il principio su cui si basa l'analisi FEM è l'equilibrio elastico. Il sistema matematico che descrive l'equilibrio elastico si compone di varie equazioni:
- 3 equazioni indefinite dell’equilibrio
- 6 equazioni di congruenza (di cui 3 indipendenti)
- 6 equazioni di Navier (descrivono la legge di Hooke)

L'analisi FEM risolve il problema partendo dal principio dei lavori virtuali, calcolando, però, lo spostamento in modo approssimato.

L'equazione dei principi virtuali è

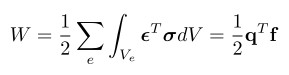
e descrive il bilancio di energia tra le forze esterne e le azioni interne.

Per poter applicare il metodo a elementi finiti, una passaggio fondamentale è la frammentazione del dominio di calcolo che genera una griglia di elementi, definita mesh.

Si passa da un numero di gradi di libertà infinito, il continuo, ad un numero di gradi di libertà finito, la mesh.
Della mesh interessano i vertici, definiti nodi.

Tramite una serie di passaggi matematici, qui tralasciati, si deduce la formulazione fondamentale:

dove

- K è la matrice di rigidezza,
- q sono gli spostamenti nodali
- f sono le forze applicate

Note le forze esterne e la matrice di rigidezza, che dipende dalle proprietà dei materiali, si risolve il sistema di equazioni cercando gli spostamenti nodali q.

Una volta notii gli spostamenti nei nodi, è anche possibile calcolare le deformazioni e le tensioni.

Il metodo FEM viene trattato agevolmente dai calcolatori moderni poiché si è trasformato il problema con una formulazione differenziale a una formulazione matriciale.